• ClasSup: Clasificación supervisada de imágenes

Acceso directo de la ayuda en Internet: ClasSup

Acceso a la aplicación desde el menú: "Herramientas | Clasificación de imágenes | Clasificación supervisada"

Presentación y opciones

ClasSup realiza una clasificación supervisada en base a clasificadores clásicos como: mínima distancia euclidiana, mínima distancia de Manhattan y máxima verosimilitud.

Clasificación supervisada de imágenes: Clasificación supervisada en base a clasificadores clásicos como: mínima distancia euclidiana, mínima distancia de Manhattan y máxima verosimilitud.

Cálculo de la divergencia transformada: Cálculo de la divergencia transformada para calcular la separabilidad entre clases.

Las signaturas que definen cada clase se leen de ficheros SGN, que típicamente habrán sido generados a partir de la aplicación AreaSGN, o bien como resultado de una ejecución de IsoMM.

Los tiempos de ejecución son muy diferentes entre los diferentes métodos clasificadores. Así, en una prueba sobre 30 ficheros BYTE de 1517 columnas * 1311 filas en un portátil con los datos leídos y escritos en un disco externo USB3, los tiempos son del orden de 5.25" en distancia euclidiana y de 6.5" en distancia de Manhattan, mientras que en máxima verosimilitud los tiempos se multiplican prácticamente por 10.

Si se desea, el clasificador también genera un ráster con la distancia (o probabilidad, según el clasificador utilizado) que ha sido utilizada como mínima distancia (o como máxima probabilidad) para clasificar cada píxel del mapa. En los clasificadores de distancia la generación de este ráster adicional puede implicar un incremento de tiempo de ejecución alrededor de un 60%, mientras que en el de máxima verosimilitud de un 11%. Al visualizar esta imagen con una paleta de grises hay que tener presente lo siguiente:

• Clasificadores por mínima distancia: Los píxeles clasificados de manera más fiable son aquellos que presentan colores más oscuros (valores más bajos), ya que están a una distancia más cercana (menor valor) al centro de la clase finalmente asignada. Así mismo, si se ha efectuado la clasificación indicando que se permite clasificar el píxel aunque no disponga de información en todas las variables, aquellos píxeles clasificados en base a menos variables (porque en algunas de ellas se encuentran valores sindatos) pueden presentar valores más bajos simplemente porque su dimensionalidad es menor y, por tanto, eso puede inducir erróneamente a pensar que su fiabilidad es más alta.
• Clasificadores por máxima verosimilitud: Los píxeles clasificados de manera más fiable son aquellos que presentan colores más claros (valores más altos), ya que presentan una probabilidad de pertenencia más alta a la clase finalmente asignada. Como en el caso anterior, si se ha efectuado la clasificación indicando que se permite clasificar el píxel aunque no disponga de información en todas las variables, aquellos píxeles clasificados en base a menos variables (porque en algunas de ellas se encuentran valores sindatos) pueden presentar valores más altos simplemente porque su dimensionalidad es menor y, por lo tanto, esto puede inducir erróneamente a pensar que su fiabilidad es más alta. Por otra parte, y dado que los valores de probabilidad pueden llegar a ser muy y muy diferentes (diversas órdenes de magnitud), se sugerimos utilizar CalcImg para aplicar un logaritmo en base 10 a los valores de las celdas de toda la imagen, la cual cosa permite tener una visualización más fácilmente comprensible. Debe recordarse también que en los comentarios de los aspectos técnicos de los metadatos se pueden encontrar factores de escalado que el MiraMon haya aplicado con el fin de poder encajar los valores de probabilidad en una imagen de tipo float.

En el caso de los clasificadores de mínima distancia se trabaja a partir de los centros de clases deseados. Si se desea trabajar con distancias normalizadas, se deben normalizar las variables de entrada.
En el caso de máxima verosimilitud se utiliza el criterio clásico de probabilidad Bayesiana a partir de los centros de clases deseados y sus matrices de variancia-covariancia.

Orientación sobre el significado de las distancias utilizadas en los procesos de clasificación

En algunas opciones del ClasSup, así como en otros clasificadores como IsoMM o kNN, se hacen cálculos de distancias estadísticas como la distancia euclidiana. En este caso se calcula la distancia euclidiana desde un píxel problema a unos ‹ ‹ valores centrales de referencia › › los que pueden ser el vector de medias de un centro de clase (por ejemplo en el caso de un clasificador por mínima distancia o al IsoMM), o pueden ser el vector de valores de un píxel de entrenamiento (por ejemplo en un clasificador kNN).

Estas distancias para la categoría "ganadora" se pueden obtener, en cada píxel, en el fichero de distancias que proporcionan algunas aplicaciones de clasificación digital de imágenes de MiraMon. La tabla siguiente muestra cómo interpretar varios valores de estas distancias; en todos los casos se trata de una clasificación con 36 variables y en la que en algunos píxeles en lugar de hacerse la clasificación con 36 variables se ha tenido que hacer con 24 variables (por ejemplo porque en alguna de las diferentes fechas utilizadas para la clasificación, en aquellos píxeles había nubes). Además, las variables presentan valores reales (no enteros) acotados entre 0 y 100; un ejemplo de esta transformación sería que los píxeles de una variable que es un índice de vegetación de diferencia normalizada, NDVI, típicamente, entre -1 y 1, se han transformado (multiplicándolos por 50 y sumándoles 50) para que sus valores estén entre 0 y 100; un segundo ejemplo sería que bandas de reflectancia, típicamente entre 0 y 1, se han convertido en valores entre 0 y 100 (multiplicándolos por 100 y convirtiéndolos en porcentajes de reflectancia).

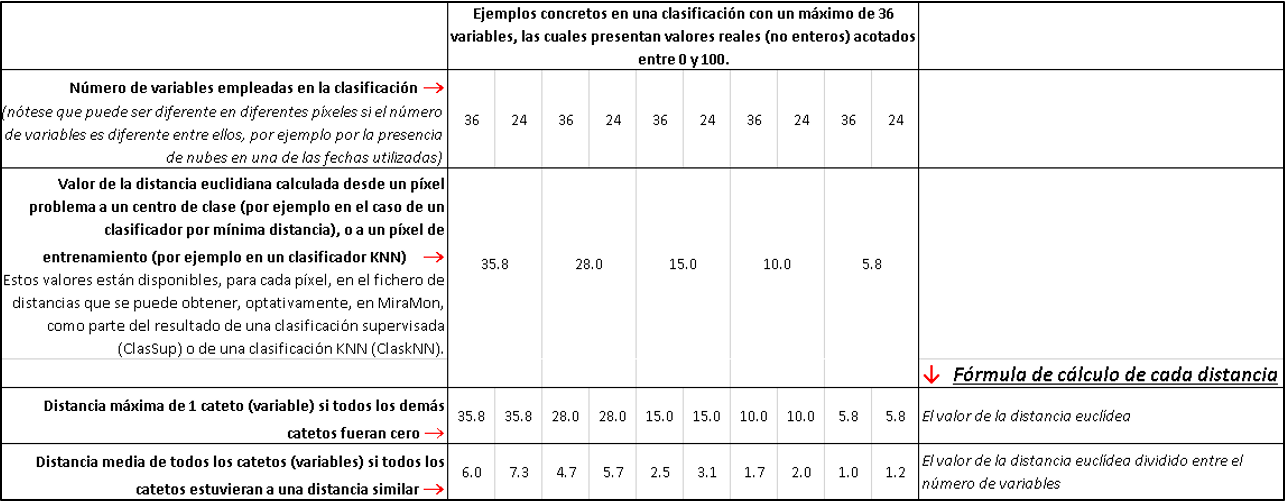
Se propone interpretar una distancia 35.8 obtenida en un píxel clasificado gracias a 36 variables disponibles. En este caso se puede imaginar que la situación puede oscilar entre que el píxel problema sea "medianamente lejos" de los valores centrales de referencia referido más arriba, o que el píxel sea muy cercano (prácticamente a distancia 0) de todas las variables utilizadas, excepto de una, que acumule prácticamente toda la distancia. En el primer caso, en la tabla se observa que la distancia hay que interpretarla como una distancia media de 6.0; realmente es bastante probable que el píxel esté mal clasificado, porque con diferencias espectrales medias, en todas aquellas variables que son respuestas en bandas espectrales en las diferentes fechas en que se han captado las imágenes, de un 6% de reflectancia, difícilmente el píxel es "similar" a la clase. En el segundo caso, en la tabla se observa que la distancia de una de las variables es 35.8 (sobre un recorrido total de 100); realmente también es bastante probable que el píxel esté mal clasificado si en una de las variables tiene un valor tan alejado del valor de referencia. Si este valor de distancia 35.8 ha sido obtenido en un píxel clasificado gracias a 24 variables disponibles, la situación de "distancia media a las diferentes variables" todavía es peor, porque pasa a ser de un 7.3 en lugar de un 6.

A continuación se puede interpretar una situación en el otro extremo: un píxel clasificado con una distancia 5.8 en base a 36 variables. Como se puede ver en la tabla, la distancia media es sólo de 1.0, es decir, sumamente cercana, y si fuera una sola de las 36 variables que fuera muy diferente mientras las otras fueran prácticamente idénticas, esta variable "discordante "sólo estaría a una distancia 5.8 (en un recorrido total de 100). Si el píxel se ha clasificado gracias a 24 variables disponibles la situación no es mucho peor: en el caso de distancia media se obtiene un valor de 1.2, que también indica una similitud media muy cercana en las 24 variables.

El resto de casos intermedios de la tabla pueden ayudar a entender, en los mismos términos, en casos en que se obtengan valores de distancia intermedios entre los dos ejemplos comentados (35.8 y 5.8).

Ni el número máximo de variables a considerar ni el tamaño de los ficheros están acotados excepto por las capacidades del sistema. Por ejemplo, en septiembre de 2013 se hicieron clasificadores de máxima verosimilitud en base a 47 imágenes integer de 8115 columnas x 8757 filas, con resultados satisfactorios en unos 90' de ejecución a pesar de que contenían valores sindatos y que también se generaba una imagen de probabilidades simultánea a la clasificación en sí.

Adicionalmente, la aplicación permite el cálculo de la Divergencia Transformada (DT), que en lugar de hacer una clasificación escribe en un fichero los valores de las matrices de covariancia y de correlaciones para cada clase, así como la DT entre todas las signaturas (clases) proporcionadas. Según Swain (1973), cuando DT=2 la probabilidad de separación entre clases alcanza valores > 90%.

Para información técnica adicional, se pueden consultar los comentarios de la aplicación IsoMM.

Por defecto esta aplicación carga todas las imágenes en memoria, lo que le permite realizar los procesos de manera más ágil. Sin embargo, en ordenadores con pocos recursos respecto del tamaño de las imágenes esta estrategia puede no ser viable. Es por ello que la opción "No cargar las imágenes a clasificar en memoria" permite indicar a la aplicación que en los procesos mantenga en memoria sólo aquellos datos que necesita en cada momento, ni que esto implique una ralentización de la ejecución. La aplicación conmuta automáticamente a este modo si no tiene suficiente memoria disponible, por lo que habitualmente no es necesario activarlo expresamente.

Esta aplicación está paralelizada, tanto en las versiones de 32 como de 64 bits, con lo cual es posible que distribuya el trabajo entre los núcleos de procesador disponibles en el ordenador donde se ejecuta. Si, por ejemplo, se dispone de un ordenador con dos procesadores de 20 núcleos cada uno, se puede conseguir dividir casi entre 40 el tiempo necesario para obtener los resultados, utilizando todos los núcleos disponibles, lo que se puede hacer con el parámetro correspondiente en un valor indicado por "MAX"; cuando se indica que el número de núcleos a emplear es MAX, la aplicación utiliza todos los núcleos. Sin embargo, a veces se puede preferir no comprometer toda la capacidad de cálculo del ordenador e indicar SUB_MAX (dejará un procesador libre para otras cosas que se estén haciendo) o indicar un valor numérico concreto inferior, en todos los casos a través de la opción "Número de núcleos de procesador a utilizar". Pedir más núcleos que los realmente disponibles es posible, creando otros virtuales, pero esto no acelera el procesado, sino al contrario. El Administrador de tareas de Windows permite conocer de qué número total de núcleos dispone el ordenador, y también puede saberse ejecutando la aplicación en modo MAX, ya que indicará por pantalla cuántos núcleos está utilizando.

Para más información se puede consultar la siguiente referencia:

Swain, P.H. (1973) A Result from Studies of Transformed Divergence. LARS Tech Report Number 050173. https://docs.lib.purdue.edu/larstech/42/

Caja de diálogo de la aplicación

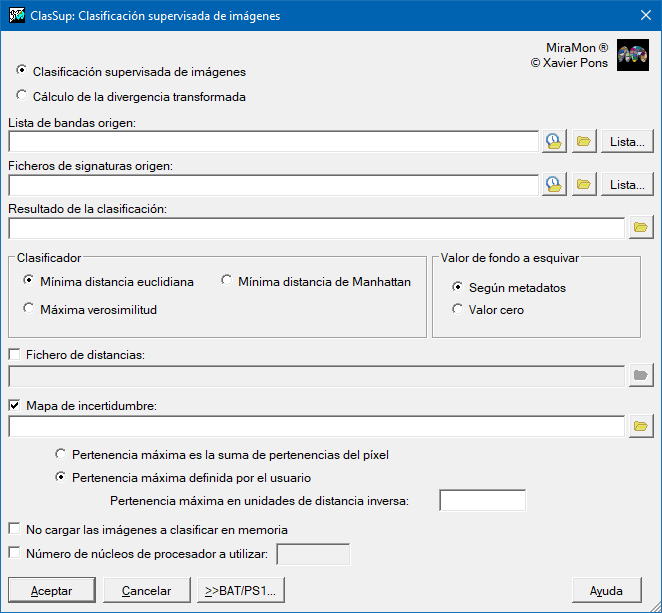Caja de diálogo de ClasSup