Summary description of the method
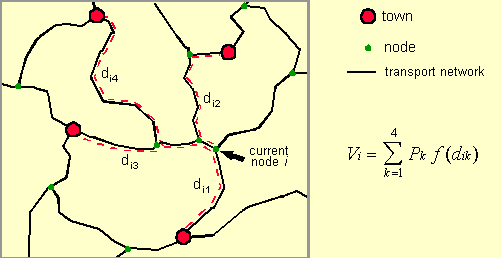
The method for the development of population rastergrids consists of the following steps. The most important inputinto the model is information about the transportation networkconsisting of roads, railroads and navigable rivers. The secondmain component is information on urban centers. Data on the locationand size of as many towns and cities as can be identified arecollected, and these settlements are linked to the transport network. This information is then used to compute a simple measure ofaccessibility for each node in the network. The measure is theso-called population potential which is the sum of thepopulation of towns in the vicinity of the current node weightedby a function of distance, whereby network distances rather thanstraight-line distances are used. The following figure illustratesthe computation of the accessibility index for a single node.
The computed accessibility estimates for each nodeare subsequently interpolated onto a regular raster surface. Raster data on inland water bodies (lakes and glaciers), protectedareas and altitude are then used to adjust the accessibility surfaceheuristically. Finally, the population totals estimated for eachadministrative unit (as described in the first part of this documentation)are distributed in proportion to the accessibility index measuresestimated for each grid cell. The resulting population countsin each pixel can then be converted to densities for further analysisand mapping. Each of these steps will now be described in moredetail. There are few data sources that provide consistent,geographically referenced base data layers for large areas suchas an entire continent. The transportation infrastructure datafor this project was constructed using the following data sets: major roads from the World Boundary Databank II (WBDII), minorroads from the Digital Chart of the World (DCW), railroads aswell as major navigable waterways from WBDII. WBDII originatedat the U.S. Central Intelligence Agency and an Arc/Info versionis available from the Environmental Systems Research Institute(ESRI). The nominal scale of WBDII is 1:3 million. The scaleof the DCW base maps (the Operational Navigational Charts) is1:1 million. Since we also used DCW for the international boundariesin the administrative unit data layers and since WBDII and DCWappear to share common ancestors, a good fit exists between theindividual data layers.
A brief technical discussion is now required to clarifythe structure of the transportation data. After merging the individualcomponents of the transport network into one data layer thereare still no connections between the individual components (e.g.,railroads and rivers). To allow the model to choose the mostefficient means of transport at any point in the network, theintersections between the individual transport layers need tobe found. This is a standard GIS operation that results in awell-structured data layer of arcs (or links) representingroads, railroads or rivers. These are connected by nodeswhich are intersections of two or more arcs of different or similartypes. Nodes, of course also represent the end of an unconnectedarc.
The program used for calculating accessibility producesan estimate for each node in the network. The problem in an applicationwhere the network is sparse in many regions is that no valuesare derived for areas that are not connected to the network. In the Africa application this applies to large areas, for example,in the Northern and Southern African desert regions. Also, WBDIIand DCW only include fairly important transport features thatare relevant at a cartographic scale of 1:1 or 1:3 million. Onesolution is to calculate the accessibility index for the centerof each grid cell of the subsequently generated output raster. From each grid cell, the distance to the closest transport featurecould be calculated and added to the network distances to theclosest towns. This approach was used by Geertman and van Eck(1995).
However, this approach is not realistic where theclosest access point to the transport network is at a locationwhich is actually far away from urban centers. Another networkaccess location may be further away from the grid cell initially,but better connected to major towns. To evaluate different optionsof network access for each grid cell would be impractical, andwe therefore chose a different approach. In areas where the transportnetwork is sparse, auxiliary arcs were added which could be thoughtof as "feeder roads". Essentially, this implies thatpeople who may be living in these remote areas are using trailsor tracks to get to the main transport network first and thencontinue their travel to the nearest city along the fastest routes. The algorithm automatically determines which network access isoptimal in minimizing overall travel times.
It would be straightforward to use simple networkdistance for the calculation of accessibility. However, differentarcs representing various transportation modes are associatedwith quite different travel speeds. For example, a kilometertravel on a paved road will take much less time than the samedistance on a river. Instead of simple distance, we thereforeused cumulative travel time as the weight in the accessibilitycalculation. Each arc in the resulting complete transportationnetwork is associated with an estimate of average travel speedthat is thought to be possible. Major, surfaced roads from WBDIIare assumed to allow for a travel time of 90km/h, minor roadswere assigned a speed of 60km/h, 50km/h are used for railroads,20km/h for navigable rivers, and 5km/h for the auxiliary networkaccess routes. For each arc, we calculated the real-world distancein kilometers.
However, all data layers are referenced in geographic(latitude/longitude) coordinates and no map projection is ableto represent real-world distances in all directions with sufficientaccuracy for large regions. We therefore calculated the correctlength of each arc as the sum of the great-circle distances ofall individual segments that make up the arc between two nodes. The time it takes to traverse each section of the transport networkis then simply its length in km divided by the travel speed associatedwith the specific mode of transport.
The accessibility index is the sum of the populationtotals of the towns in the vicinity of the current location weightedby the network travel time ("distance") to those towns. Data on the location and size of urban centers were collectedfrom a range of sources. Based on the World Cities PopulationDatabase developed by Birkbeck College and distributed by UNEP/GRID,a considerable number of additional town populations were identifiedfrom UN publications, gazetteers and yearbooks, and national censusreports. The location of towns was determined from the gazetteerin the Times Atlas or from published maps. Altogether, about1800 cities were identified from all sources. Where populationfigures for the town were available for more than one time, estimatesfor the four standard time periods were produced in the same wayas the district population figures. Where only one figure wasavailable, the corresponding national-level average annual urbangrowth rates published in the UN World Urbanization Prospects(1994 revision, UN Population Division) were used. During the modeling, it became clear that despitethe considerable effort that went into the development of theurban database, the available detail was still insufficient inall but a few countries. Generally, population figures are publishedonly for the largest cities in a country - i.e., those with populationtotals larger than 100,000. We therefore added additional townswhose locations were determined from available maps and atlasesand whose population figures were estimated using a simple heuristicbased on the rank-size rule. Although this rule helps us to determinehow many towns with a given population total might exist, thereis no way of knowing which town should be associated with whichpopulation figure. We therefore assigned the population totalsheuristically keeping patterns suggested by central place theoryin mind. For example, major regional centers should be surroundedby several minor centers with a correspondingly lower population. This procedure is clearly subject to significantjudgmental error. Although the errors introduced cannot be determined,we expect that the added benefit of using additional towns inthe accessibility calculation far outweighs the potential errorintroduced in the resulting accessibility index. In fact, sincemost of these auxiliary towns have relatively low population totals(since the major towns are already accounted for), the error introducedby this heuristic estimation procedure may well be small; i.e.,not much larger than the ordinarily expected error in publishedurban population figures. Still, in a future modeling efforta more formal procedure could be developed that combines the empiricalevidence that forms the basis of the rank-size rule and centralplace theory to provide a more replicable estimate of the urbanhierarchy in a country.
Towns need to be connected to the transport networkto enable the accessibility calculation algorithm to find theclosest towns for each node in the network. Each settlement wastherefore assigned to the network node closest to its recordedlocation.
For the actual accessibility calculation we useda stand-alone program written in the C programming language. This program reads the entire network definition which consistsof (a) the identifiers for each node and the population size ofthe town that corresponds to the node - zero in most cases, indicatingthat no town is located at the node -, and (b) the identifiersof the two nodes that define each arc and the travel time requiredto traverse the arc.
A further option of the program that allows for consideringthe direction of travel along an arc was not used. This impliesthat there are no "one-way streets" and that traveltime is the same regardless of which way one travels. This assumptioncould be relaxed since, for example, travel speeds are lower up-riverthan down-river, but the added gain in realism will not compensatefor the additional effort required in defining these details. Also, no further assumptions are made about modal choice. Inmoving through the network, an imaginary traveler may change hisor her means of transport at will. This is unrealistic sincea switch, say from road travel to a train and on to a boat, areall associated with delays. Even so, in order to keep the modelsimple (and run-times manageable) we did not introduce a penaltyfor switching the transport mode. A modification relevant toan application in a regional setting was made, however. For anyarc that crosses an international boundary, the travel time wasincreased by 20 minutes reflecting delays in border crossings. This added travel time could be varied depending on the relationsbetween two neighboring countries. This would either requiresubjective judgment or very detailed information on the permeabilityof international borders.
For each node in the network, the program now findsthe network path to each of a specified number of towns that resultsin the lowest overall travel time. In the initial program specification,all towns reached within a user-defined specified travel time(e.g., 5 hours) were determined. However, in areas where townsare sparsely distributed and the number of nodes and arcs is large,this resulted in unacceptably long run-times. Instead, we modifiedthe program to find the closest four towns or less if fewer thanfour towns were accessible within a more generous threshold traveltime. This also makes the index somewhat more comparable acrosslarge areas, since the previous specification resulted in theaccessibility index for some densely urbanized areas to be basedon fifty or more towns, while other regions would only containtwo or three.
For the shortest path calculation the program usesthe standard Dijkstra algorithm. The program section used forthis search consists of a modified version of a fast implementationof this algorithm developed by Tom Cova, a transportation GISspecialist at NCGIA. The Dijkstra algorithm evaluates the networkstructure around the current location starting from the centerand reaching out further and further. For applications in whichonly one origin-destination pair is of interest, this is inefficientand various modifications have been suggested to speed up thesearch. In this application, in contrast, the interest is infinding the shortest path to all towns within the vicinity andthe Dikstra's "shortcoming" is actually a bonus. Theslightly modified algorithm thus "collects" towns asit ventures out from the originating node. Once four towns havebeen found and the program has determined that all additionalconnected arcs will not lead to a town that is closer than thosealready found, the search is terminated and the town populationsand travel times are passed to a program section that calculatesthe accessibility measure.
This measure is the sum of the town populations weightedby a negative exponential function of travel time ("distance"). I.e.,
where Vi is the accessibility estimatefor node i, Pk is the population of townk, The accessibility index that is available for eachof the nodes in the network needs to be converted into a regularraster grid. We used a simple inverse distance interpolationprocedure that resulted in a relatively smooth surface. A problemwith this technique is that interpolated values will not falloutside the range of the values recorded at the neighboring nodelocations. In analogy to interpolating elevation data: if recordedvalues are available only for locations on the slope of a mountainbut not at the peak, the interpolated value for the summit locationwill be underestimated. Conversely in our application, if valuesare recorded only for network nodes, but not for areas that areremote from transport routes (e.g., deserts), then using the neighboringnode values for interpolation will overestimate the accessibilityfor the remote location.
Yet, experiments with other interpolation proceduresdid not result in satisfactory results. Thin plate spline interpolationmay be more appealing theoretically since it would allow valuesat interpolated locations to fall below (or above) those thatare recorded at neighboring locations if the overall tension surfacesuggests a corresponding trend. However, the values estimatedfor some locations were clearly out of the range of what wouldbe reasonable. Given the large number of nodes introduced inremote areas by adding the auxiliary access routes, we considerthe simple inverse distance interpolation to be sufficiently accurate.
Three additional data sets were used to adjust theresulting accessibility index grid: inland water bodies, protectedareas, and elevation. Lake areas were masked and grid cells thatfell onto a glacier were assigned an accessibility value of zero. This information was derived from the WDBII (i.e., ArcWorld)lakes layer.
GIS data layers on protected areas were obtainedfrom the World Conservation Monitoring Center (WCMC). Unfortunately,little information about each protected area was available besidesits name, such that it was impossible to relate, for example,protection status to an estimate of how much the areas may stillbe used and inhabited by people. We reduced the accessibilityindex for grid cells that fell into national parks to 20 percentof the original value and for areas falling into forest reservesto 50 percent. These values are subjectively determined to allowfor the fact that the protection of protected areas is not alwaysperfect. Since most of these parks are in remote region, thechange in predicted population densities that would be introducedby varying the adjustment factors should be small.
In contrast to the Asia population surfaces, no adjustmentfor elevation was made in the Africa data sets. Only few areasin Africa are uninhabitable due to high altitude. These areas(e.g., Mount Kenya or Kilimanjaro) are also protected areas andhave thus been considered already.
The distribution of the population total availablefor each administrative unit over the grid cells that fall intothat unit is straightforward. The accessibility values estimatedfor each grid cell serve as weights to distribute population proportionately. First the grid cells in the accessibility index are summed withineach district. Each value is divided by the corresponding districtsum such that the resulting weights sum to one within each administrativeunit. Multiplying each cell value by the total population yieldsthe estimated number of people residing in each grid cell. Thestandardization of the accessibility index implies that the absolutemagnitudes of the predicted access values are unimportant - onlythe variation within the administrative unit determines populationdensities within each district.
Again, we have to take account of the fact that allGIS data layers and raster grids are referenced in latitude/longitudecoordinates. This means that grid cells further away from theequator represent a smaller real-world area than grid cells closeto it. For example, a 2.5 minute grid cell has a real-world areaof 10.8 square km at 60 degrees latitude, of 18.6 square km at30 degrees and of 21.4 square km at the equator. We thereforeweighted the accessibility index value for each grid cell by theactual area of the grid cell before standardizing the values withineach district.
Because only the relative magnitudes of the accessibilityindex are important in distributing total population, and sincemost administrative units are fairly small, the error introducedby the distortions of the geographic coordinate system will usuallybe insignificant. However, in areas where the available resolutionof the administrative units is fairly low, the difference in theactual areas of grid cells within a district that are locatedfurther away from the equator compared to those closer to theequator can be relatively large. For example, in Asia which reachesinto much higher latitudes than Africa, the resulting differencein predicted population densities using undadjusted and adjustedaccessibility values reached up to eight people per square km. From the grid cells of total population, population density imagesare created by dividing the population counts estimated for eachgrid cell by the real-world area in square km of that cell.
Evaluating the accuracy of this interpolation methodis difficult in the absence of very high resolution populationdata (e.g., by enumeration areas) that could be used as a benchmark. For the Asian database a simple experiment was conducted in whichstate level population figures for India were interpolated. Thetotal population allocated to each district could then be comparedto the actual district figures. The differences are acceptablein relatively homogeneous regions but are obviously quite largein areas where population distribution is very scattered suchas in high mountain or desert regions. The same results couldbe expected for Africa. The model will work better, the moredetailed the administrative data, the more urban population figuresare available, and the more homogeneous the population is distributed.
[ Next Section | African Population Distribution Database |
<URL: http://grid2.cr.usgs.gov/globalpop/africa/part2.htm>
Construction of the transportation
network
Setting up urban data
Run accessibility calculation
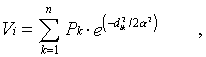
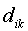 is the travel time/distancebetween node i and town k, and is the distanceto the point of inflection in the distance decay function. Thisparameter was set to one hour in this case which means that theinfluence of a town one hour away decreases to about 60 percent,and a town two hours away will only contribute 14 percent of itstotal population to the accessibility index. Rather than usingtotal urban population, we applied a square root transformationto the population figures, implying that each additional personliving in a city has an increasingly lower influence. This transformationavoids an exaggerated influence of very large mega-cities whilebeing less of an equalizer than the more common log-transformation.
is the travel time/distancebetween node i and town k, and is the distanceto the point of inflection in the distance decay function. Thisparameter was set to one hour in this case which means that theinfluence of a town one hour away decreases to about 60 percent,and a town two hours away will only contribute 14 percent of itstotal population to the accessibility index. Rather than usingtotal urban population, we applied a square root transformationto the population figures, implying that each additional personliving in a city has an increasingly lower influence. This transformationavoids an exaggerated influence of very large mega-cities whilebeing less of an equalizer than the more common log-transformation.
Interpolation
Adjustment of the accessibility
measure
Distribution of population
 UNEP/GRID-Sioux Falls ]
UNEP/GRID-Sioux Falls ]
Last modified: 19 February 1997.
Please address any comments or suggestions to
 uwe@ncgia.ucsb.edu.
uwe@ncgia.ucsb.edu.