• RegMult: Regressió multivariant i interpolació de residus

Accés a aquest text d'ajuda com a pàgina web: RegMult

Presentació i opcions

El model aplica regressió lineal múltiple de forma que la variable dependent Y s'intenta obtenir de les variables independents x_n, a partir d'una expressió com ara:

Els coeficients a₀, a₁,... a_n s'ajusten per mínims quadrats. L'aplicació ofereix la possibilitat d'afegir una interpolació espacial dels residus resultants de la regressió múltiple, de forma que en molts casos es millora el poder predictiu per tal com la interpolació pot recollir una part important de la variància no explicada pel model de regressió múltiple.

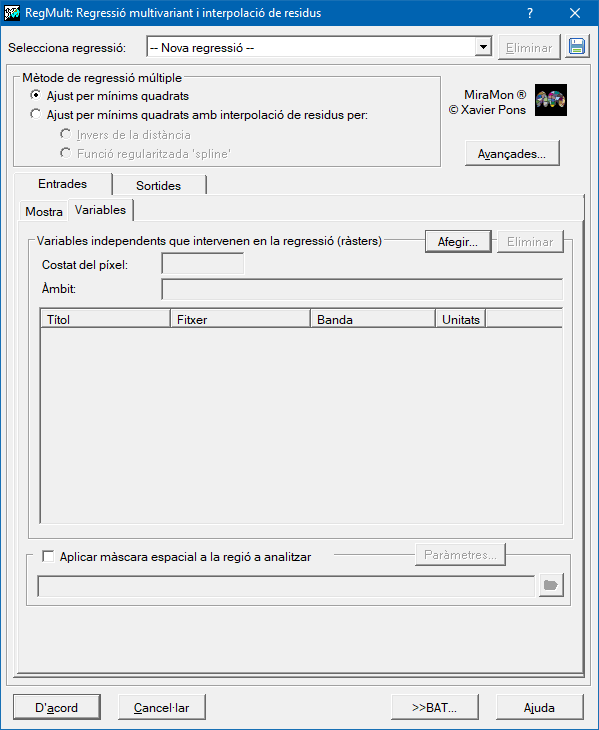
Per tal de determinar els coeficients de la regressió és necessari proporcionar un conjunt de mostres on és coneguda alhora la variable dependent en localitzacions concretes (puntuals) i el conjunt de les possibles variables independents. Aquestes mostres es proporcionaran o bé en un fitxer de punts estructurat PNT, o en una taula en format DBF, o bé en una taula en qualsevol altre format accessibles mitjançant un driver ODBC (Open DataBase Connectivity). Les variables independents caldrà proporcionar-les com a ràsters en format IMG del mateix àmbit geogràfic i costat de píxel. El resultat predictiu serà també un ràster en format IMG.

El procés per a elaborar el ràster resultat consta de dues fases (o de només una única fase en la versió simplificada de l'algorisme): la regressió i la interpolació.
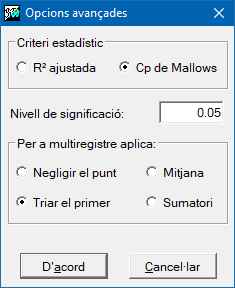
El procediment de regressió és, de fet, un procés iteratiu d'ajust de totes les regressions possibles: des de la regressió amb totes les variables independents inicialment introduïdes fins a les regressions amb una única variable independent. Analitzant els paràmetres estadístics de cada regressió i en funció del criteri escollit, millor R² ajustada o C_p de Mallows, s'obté la que es considera millor regressió de totes (sempre que se superi el mínim llindar de significació exigit).

Durant el procediment de selecció de la regressió òptima, l'aplicació informa dels paràmetres estadístics de la regressió amb totes les variables independents introduïdes i dels paràmetres estadístics de la regressió seleccionada (evidentment només si les dues solucions no són la mateixa) i així poder avaluar com millora la regressió seleccionada en eliminar alguna variable que s'ha detectat que és poc significativa.
Si l'usuari ha seleccionat només l'opció de regressió multivariant, el model resultat es generarà en calcular a tot l'àmbit d'estudi la solució de la regressió seleccionada a partir dels coeficients ajustats aplicats a les variables independents, les quals estan definides necessàriament a tot l'àmbit d'estudi.

Si l'usuari ha seleccionat obtenir el model amb l'algorisme complet (regressió+interpolació de residus), hi haurà una segona fase amb el càlcul dels residus de la mostra de punts d'ajust. Els residus s'obtenen en calcular les diferències entre el model predit per la regressió multivariant i el valor conegut de la variable dependent. Aquests residus coneguts només en les localitzacions dels punts d'ajust, s'estendran a tot l'àmbit d'estudi mitjançant un procediment d'interpolació. L'usuari podrà triar entre dos mètodes d'interpolació: Invers de la distància ponderada o Funció regularitzada spline. Podeu veure els paràmetres i les característiques d'aquestes dues metodologies a InterPNT.htm.
És important realitzar la cerca del joc de paràmetres que donarà lloc a una interpolació dels residus òptima. Els resultats de la interpolació, i de retruc del model en conjunt, poden variar de forma significativa en aplicar un joc de paràmetres o un altre. En aquest sentit, és molt aconsellable reservar una mostra independent dels punts amb dades per a realitzar el test de verificació. Aquest test consistirà fonamentalment a calcular l'RMS (arrel de la mitjana del quadrat dels errors) total dels punts de test, verificant que no hi hagi algun punt en particular amb un error excessivament elevat. Serà aquest indicador (RMS) el que donarà una bona base per acceptar un determinat joc de paràmetres. Altres criteris complementaris podrien ser avaluar la presència d'artefactes en la interpolació, si s'aprecia algun error sistemàtic, etc.

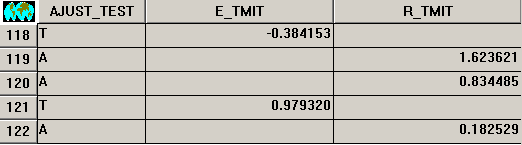
Per a facilitar tota aquesta anàlisi, que ha de donar lloc al millor model possible, l'aplicació ofereix la possibilitat de generar dues capes resultat. La primera d'aquestes capes és una capa vectorial de punts, que conté aquells punts vàlids amb dades que, o bé participen en l'ajust i posteriorment s'usaran per interpolar els residus coneguts, o bé serveixen de test per a validar la solució interpolada. Per als punts de test s'informa, en la seva base de dades, de la diferència entre el valor conegut i el valor predit pel model (regressió+interpolació), i per als punts d'ajust s'informa del residu obtingut com a diferència entre el valor conegut i el valor predit (només regressió). La il·lustració següent mostra aquests detalls.

L'altra capa resultat, opcional i informativa, és el ràster resultat de la interpolació de residus. Una inspecció d'aquesta capa servirà per analitzar en profunditat la fase d'interpolació deslligada de la regressió. Pot servir per analitzar si la interpolació ha donat lloc a artefactes poc desitjats, sortides excessives de rang, zones amb excessiva variabilitat, etc. També pot ser una interessant font per a conèixer i investigar les zones que presenten variabilitat no recollida adequadament per les variables independents.

En principi, tots els punts que tinguin dades vàlides dins la zona d'estudi del fitxer PNT amb les mostres s'usaran o bé com a punts d'ajust o bé com a punts de test. Tanmateix, l'aplicació permet filtrar aquelles dades que no es considerin apropiades en funció d'aplicar restriccions sobre la seva base de dades. Si la mostra es dóna en absència de capa gràfica explícita, on llavors cal necessàriament definir els camps amb les coordenades, aquestes restriccions poden definir-se a partir de construir una sentència SQL (Structured Query Language). Una vegada seleccionat el total de la mostra a usar caldrà definir com se subdividirà en punts d'ajust i test.

La tria de quins punts de la mostra seran punts d'ajust i quins seran de test, pot deixar-se com a opció aleatòria indicant només quina proporció (%) correspondrà a punts d'ajust i quina a punts de test. Aquesta tria aleatòria pot originar-se a partir d'una llavor fixa i per tant donarà lloc a submostres reproduïbles, o a partir d'una llavor variable per a obtenir submostres diferents en cada nova execució. També s'ofereix la possibilitat de decidir aquesta tria governada per un camp de la seva base de dades: en aquest camp caldrà assignar un valor A pels punts d'ajust i un valor T pels punts de test. També s'ofereix la possibilitat de fer una validació encreuada. En aquest cas el ràster resultat s'obté usant tots els punts com a punts d'ajust i, per a fer el test, es duen a terme una sèrie d' iteracions, en nombre igual al nombre de punts, on en cada una d'elles es torna a fer l'ajust però deixant fora un punt per fer el test. L'RMS final es calcula com l'arrel quadrada de la mitjana dels errors de cada iteració prèviament elevats al quadrat. Aquest tipus de validació és especialment interessant quan la variable dependent té poques mostres i no es pot prescindir de cap per usar-les com a punt de test. Usant la validació encreuada totes les mostres són a la vegada d'ajust i de test.

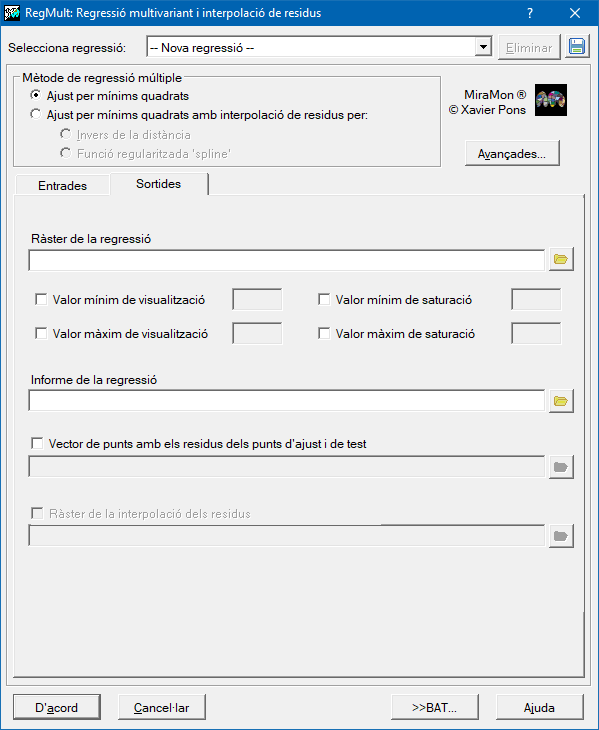
Els dos fitxers resultat obligatòries són un fitxer de text pla, que recull informació de com s'ha realitzat tot el procés complet, i un ràster amb el model predictiu.
El fitxer de text informa de quines opcions ha triat l'usuari, quins són els coeficients ajustats de la regressió, tant els que s'usen per a reproduir el model multivariant com els coeficients normalitzats (reduïts a rangs comparables de mitjana 0 i desviació 1) per a poder analitzar la influència de cada variable independent dins el model, quines variables independents s'han finalment descartat i quins són els estadístics principals de la regressió seleccionada i de la completa; finalment s'informa de la qualitat del model mitjançant l'RMS dels punts de test, que també queda documentat en les metadades de la capa resultat.

El ràster IMG resultat del model predictiu tindrà el mateix àmbit geogràfic i costat de píxel que els ràsters de les variables independents; es pot delimitar, mitjançant una màscara d'exclusió, en quines zones no és necessari conèixer el valor resultat (s'assignarà sensedades). El fet d'evitar calcular la solució del model en aquestes zones pot accelerar considerablement la velocitat d'execució. També es poden definir uns valors extrems de visualització (mínim i màxim) que permetran realitzar mapes visualment comparables en aconseguir d'aquesta manera mantenir constant l'assignació entre el rang de valors i els colors de la paleta assignada.

Per a més informació es pot consultar la següent referència:

Ninyerola M, Pons X, Roure JM (2000) A methodological approach of climatological modelling of air temperature and precipitation through GIS techniques. International Journal of Climatology 20: 1823-1841. DOI: 10.1002/1097-0088(20001130)20:14<1823::AID-JOC566>3.0.CO;2-B. https://rmets.onlinelibrary.wiley.com/doi/epdf/10.1002/1097-0088(20001130)20:14<1823::AID-JOC566>3.0.CO;2-B.

Caixa de diàleg de l'aplicació

Caixa de diàleg del RegMult