-
 RegLog: Regressió logística
RegLog: Regressió logística
Accés a aquest text d'ajuda com a pàgina web: RegLog
Presentació i opcions
Aquesta aplicació permet generar un model explicatiu i predictiu d'una variable espacial dicotòmica Y en funció de n variables espacials independents Xn quantitatives.
La variable dependent Y sempre serà dicotòmica i, per tant, els valors numèrics que prendrà seran 1 o 0 (presència/absència, si/no, èxit/fracàs...). El propòsit de l'anàlisi és predir la probabilitat que la variable Y prengui valor 1 en funció dels valors de les variables explicatives, P(Y=1|X), i avaluar la relació o efecte d'aquestes sobre la variable dependent.
L'anàlisi està fonamentada en el model de regressió logística binària multivariant el qual assumeix que la probabilitat que la variable Y prengui valor 1 segueix la distribució logística i, per tant, el seu valor pot ser estimat segons la fórmula següent, anomenada funció logística:
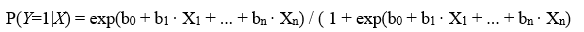
on:
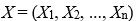 són les variables independents,
són les variables independents,
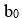 és la constant del model o terme independent,
és la constant del model o terme independent,
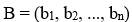 són els coeficients de les variables independents.
són els coeficients de les variables independents.
Aquesta funció és contínua i pren valors en el rang [0,1].
El vector de coeficients 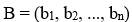 s'estima mitjançant el mètode de màxima versemblança, és a dir, els coeficients són ajustats de manera que es maximitza la funció de versemblança.
s'estima mitjançant el mètode de màxima versemblança, és a dir, els coeficients són ajustats de manera que es maximitza la funció de versemblança.
Donat que una variable dependent dicotòmica segueix una distribució binomial, la funció de versemblança per a una mostra aleatòria de N observacions s'expressa per:
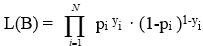
on:
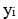 és el valor observat (1 o 0) de la variable dependent per la mostra i
és el valor observat (1 o 0) de la variable dependent per la mostra i
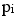 és el valor predit de la variable dependent per la mostra i,
és el valor predit de la variable dependent per la mostra i, 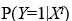 .
.
Els coeficients que maximitzin L(B) també maximitzaran la seva transformació logarítmica. Per maximitzar el logaritme de la funció de versemblança cal trobar la solució del següent sistema d'equacions no lineals:
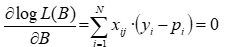
on:
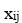 és el valor observat de la variable independent
és el valor observat de la variable independent 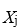 per a la mostra i.
per a la mostra i.
En l'aplicació s'ha implementat l'algoritme iteratiu de Newton-Raphson per resoldre'l.
Així doncs, per determinar els coeficients de la regressió és necessari proporcionar un conjunt de mostres on és coneguda tant la variable dependent (1 o 0) en localitzacions concretes (puntuals) com el conjunt de les possibles variables independents. Aquestes mostres es proporcionaran o bé en un fitxer de punts estructurat PNT o en una taula en format DBF o bé en una taula en qualsevol altre format accessibles mitjançant un driver ODBC (Open DataBase Connectivity). Les variables independents caldrà que siguin proporcionades com a ràsters en format IMG del mateix àmbit geogràfic i costat de píxel. El resultat predictiu serà també un ràster en format IMG.
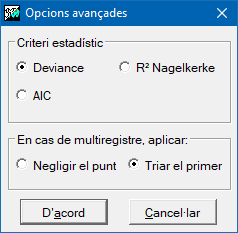
El procediment de regressió és, de fet, un procés iteratiu d'ajust de totes les regressions possibles: des de la regressió amb totes les variables independents inicialment introduïdes fins a les regressions amb una única variable independent. Analitzant els paràmetres estadístics de cada regressió i en funció del criteri escollit (menor coeficient AIC, menor estadístic Deviance o millor coeficient R2 de Naglekerke, s'obté la que es considera millor regressió de totes.
Per a més informació del model de regressió logística, del mètode de màxima versemblança i de l'algoritme iteratiu Newton-Raphson es pot consultar la següent referència:
Czepiel, S.A. (2002) Maximum Likelihood Estimation of Logistic Regression Models: Theory and Implementation https://czep.net/stat/mlelr.pdf.

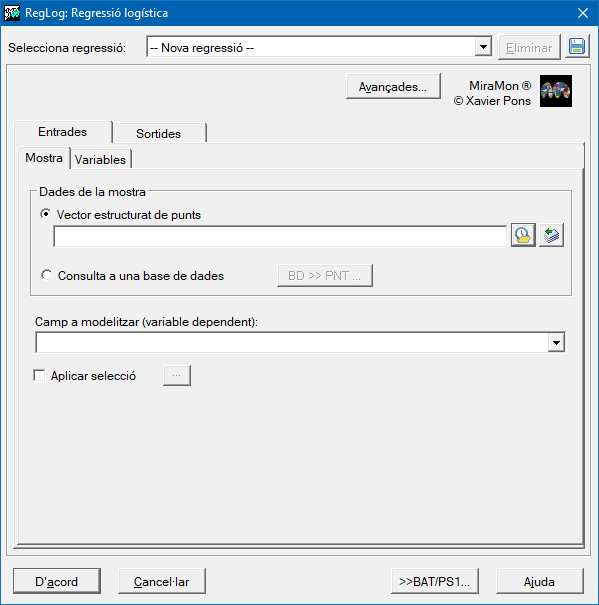
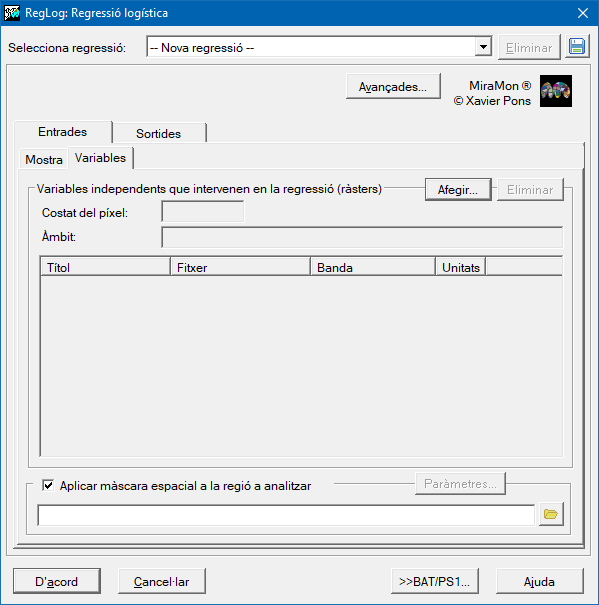
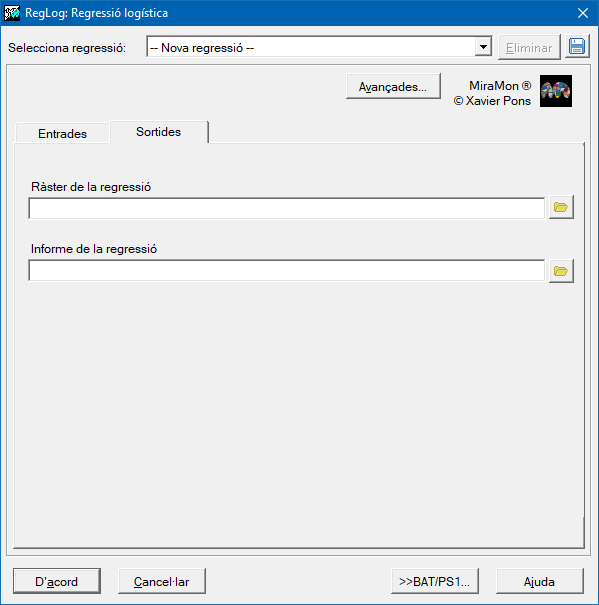
Caixa de diàleg de l'aplicació
|
| Caixa de diàleg del RegLog |

Sintaxi
Sintaxi:
- RegLog Ajust FitxMostra CampModel Criteri Multiregistre MDTSortida TXTSortida FitxVarIndep [/MOSTRA_VALORS_CRITERIS] [/CAMPY] [/MASCARA] [/CAMP_MASC] [/TAULA_MASC] [/OPER_MASC] [/CONSIDER_NODATA] [/CAMPX] [/REFSYSTEM] /ATR_MASC /PNTdeBD
Paràmetres:
- Ajust
(Opció ajust -
Paràmetre d'entrada): Actualment exclusivament pot valer 2.
- FitxMostra
(Fitxer d'entrada de la mostra -
Paràmetre d'entrada): Fitxer d'entrada corresponent a les dades de la mostra.
- CampModel
(Camp a modelitzar (variable dependent) -
Paràmetre d'entrada): Camp a modelitzar (variable dependent)
- Criteri
(Criteri estadístic -
Paràmetre d'entrada):
- 0: Totes les variables són independents
- 1: Criteri Deviance
- 2: Criteri R2 Naglekerke
- 3: Criteri AIC
- Multiregistre (Paràmetre d'entrada): Com tractar les dades d'entrada amb multiregistre, és a dir, què fer quan es té més d'un registre per cada punt:
- 0: Negligir el punt.
- 1: Triar el primer.
- 2: Calcular la mitjana dels valors.
- 3: Calcular el sumatori dels valors.
- MDTSortida
(Fitxer MDT de sortida -
Paràmetre de sortida): Fitxer MDT de sortida
- TXTSortida
(Fitxer TXT de sortida -
Paràmetre de sortida): Fitxer TXT de sortida
- FitxVarIndep
(Fitxers de les variables independents -
Paràmetre d'entrada): Fitxers de les variables independents
Modificadors:
/MOSTRA_VALORS_CRITERIS
(Mostra valors i criteris)
Mostra en pantalla informació de cada regressió. (Paràmetre d'entrada) /CAMPY=
(Camp seleccionat de les coordenades Y)
En cas de demanar la creació d'un fitxer de punts a partir de la base de dades de la mostra, és el camp seleccionat de les coordenades Y. (Paràmetre d'entrada) /MASCARA=
(Fitxer màscara)
Fitxer màscara (Paràmetre d'entrada) /CAMP_MASC
(Camp de la base de dades triada)
Quan la màscara és un fitxer estructurat, indica el camp de la base de dades triada. Per a saber més sobre els valors d'aquest paràmetre es pot consultar les consideracions del document de sintaxi general. (Paràmetre d'entrada) /TAULA_MASC=
(Taula de la base de dades triada)
Quan la màscara és un fitxer estructurat, indica la taula de la base de dades triada. Per a saber més sobre els valors d'aquest paràmetre es pot consultar les consideracions del document de sintaxi general. (Paràmetre d'entrada) /OPER_MASC=
(Operador de la projecció del camp)
Operador de la projecció del camp. Exclusivament en el cas que el fitxer màscara sigui un fitxer de polígons no estructurat. (Paràmetre d'entrada) /CONSIDER_NODATA
(Valor sensedades en màscara)
En el cas d'un fitxer màscara, considerar el valor sensedades. (Paràmetre d'entrada) /CAMPX=
(Camp de les coordenades X)
En cas de demanar la creació d'un fitxer de punts a partir de la base de dades de la mostra, és el camp seleccionat de les coordenades X. (Paràmetre d'entrada) /REFSYSTEM
(Sistema de referencia horitzontal del fitxer PNT de la base de dades)
En cas que es demani crear un fitxer PNT a partir de la base de dades de la mostra, és el sistema de referència horitzontal seleccionat per aquest fitxer. (Paràmetre d'entrada) /ATR_MASC=
(Valor seleccionat del fitxer màscara)
Valor seleccionat del fitxer màscara. Exclusivament en el cas que el fitxer màscara sigui un fitxer de polígons no estructurat. (Paràmetre d'entrada) /PNTdeBD=
(Fitxer PNT a partir d'una base de dades)
En cas que les dades de la mostra sigui el resultat d'una consulta a una base de dades, es pot demanar la creació d'un fitxer de PNT si també hi ha els identificadors /CAMPX i /CAMPY. (Paràmetre de sortida)

 RegLog: Regressió logística
RegLog: Regressió logística RegLog: Regressió logística
RegLog: Regressió logística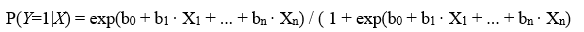
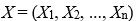 són les variables independents,
són les variables independents,
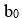 és la constant del model o terme independent,
és la constant del model o terme independent,
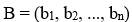 són els coeficients de les variables independents.
són els coeficients de les variables independents.
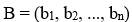 s'estima mitjançant el mètode de màxima versemblança, és a dir, els coeficients són ajustats de manera que es maximitza la funció de versemblança.
s'estima mitjançant el mètode de màxima versemblança, és a dir, els coeficients són ajustats de manera que es maximitza la funció de versemblança.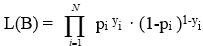
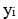 és el valor observat (1 o 0) de la variable dependent per la mostra i
és el valor observat (1 o 0) de la variable dependent per la mostra i
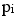 és el valor predit de la variable dependent per la mostra i,
és el valor predit de la variable dependent per la mostra i, 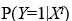 .
.
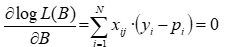
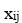 és el valor observat de la variable independent
és el valor observat de la variable independent 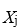 per a la mostra i.
per a la mostra i.