• AutoCor: Anàlisi d'autocorrelació espacial (Moran)

Accés directe de l'ajuda a Internet: AutoCor

Accés a l'aplicació des del menú: "Eines | Modelització i altres anàlisis | Anàlisi d'autocorrelació espacial (Moran)"

Presentació

Aquesta aplicació permet quantificar el grau d'autocorrelació espacial d'una variable en un fitxer ràster mitjançat el càlcul d'un indicador, en aquest cas a través de l'índex I(i) de Moran.

L'autocorrelació espacial és una propietat present en la distribució espacial d'una variable si els valors en qualsevol localització estan influenciats per valors de localitzacions properes (seguint la primera llei de la Geografia de Tobler https://en.wikipedia.org/wiki/Tobler%27s_first_law_of_geography). El concepte de "proper" quedarà referit al llindar d'autocorrelació, distància límit on l'autocorrelació és molt baixa o inexistent. Aquest llindar és útil per a imposar les condicions espacials idònies per al mostreig de la variable i per a aplicar determinats models estadístics associats.

L'índex I de Moran es calcula amb la següent fórmula:

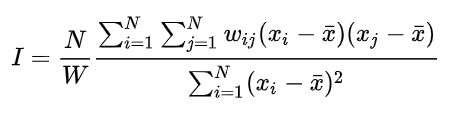
on:

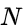és el nombre d'unitats espacials, indexades per i i j; 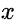és la variable d'interès; 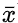és la mitjana de la variable d'interès; 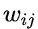és un element d'una matriu de pesos espacials amb zeros a la diagonal; 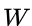és la suma de tots els elements de la matriu de pesos, és a dir:
.

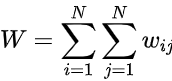La matriu de pesos formada pel conjunt de 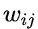es pot definir seguint el moviment de les torres dels escacs (rook en anglès), o bé seguint el moviment de la reina dels escacs (queen en anglès). En ambdós casos la matriu assigna un pes 1 a les cel·les veïnes en les direccions nord, sud, est i oest. En el primer cas s'assigna un pes 0 a les altres direccions (diagonals), mentre que en el segon cas s'assigna un pes 0.70711 (=0.5·√2) a les altres direccions.

L'autocorrelació espacial permet identificar patrons espacials diferents de patrons purament aleatoris i de patrons regulars, com un tauler d'escacs. En l'exemple del tauler d'escacs, i aplicant el criteri de pesos de 4 veïns en creu, l'índex obtingut té un valor -1; en canvi si els escacs (quadrats) blancs s'apilen a una meitat del tauler i els negres a l'altra, l'índex s'acosta a +1 a mesura que N augmenta; finalment, en una disposició aleatòria dels escacs l'índex retornat serà un valor proper a 0. Valors més petits que -1 o més grans que +1 són possibles, però habitualment corresponen a situacions molt esbiaixades de l'histograma i amb alguns valors que tenen molt pocs veïns en relació a la distància analitzada.

Per a més informació es pot consultar la següent referència:

Caixa de diàleg de l'aplicació

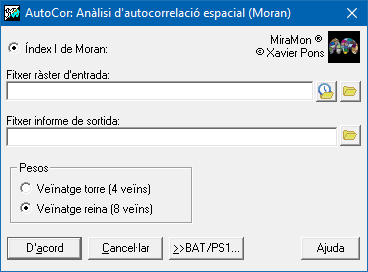Caixa de diàleg de l'AutoCor